Gravedad de Marte 🔴 - Cálculo.

Situación. ¿Cuál es el valor de la gravedad en Marte si su masa es $6,42\times 10^{23}$ kg y su radio $3397$ km?

Datos

$M_{Marte} = 6,42\times 10^{23}$ kg
$R_{Marte} = 3397 \times 10^3 m$
$G = 6.67\times 10^{-11} \dfrac{N·m^2}{kg^2}$

Resolución. Sabiendo que la gravedad de un cuerpo se calcula por medio de la siguiente expresión:

Ley de gravitación universal

$$g = G \times\dfrac{M}{R^2}$$

$$g = (6.67\times 10^{-11} \dfrac{N·m^2}{kg^2}) \times\dfrac{6,42\times 10^{23} kg}{(3397 \times 10^3 m)^2} = 3,71 \dfrac{m}{s^2}$$

Gravedad en Marte:

$$\quad g = 3,71 \dfrac{m}{s^2}$$

Explicación teórica.

Isaac Newton, durante su retiro en una granja de Woolsthorpe durante los años 1665-1666 elaboró la base de lo que hoy se conoce como la ley de gravitación universal, basándose en las leyes de Kepler sobre el movimiento de los planetas y los estudios de Galileo.

Esta ley establece que los cuerpos, por el simple hecho de tener masa, experimentan una fuerza de atracción hacia otros cuerpos con masa, denominada fuerza gravitatoria o fuerza gravitacional. Esta fuerza, explica entre otras muchas cosas, por qué orbitan los planetas.

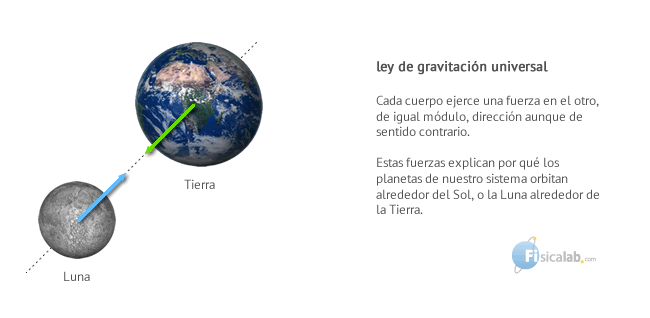
La fuerza gravitacional entre dos cuerpos es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa. Matemáticamente se expresa el módulo de dicha fuerza mediante la siguiente ecuación:

$$F_g = -G \times\dfrac{M\cdot m}{r^2}$$

donde:

📌 $G$ es la constante de gravitación universal;
(En la ley de gravitación universal de Newton, la letra G representa la constante de gravitación universal, que determina la fuerza de atracción entre dos cuerpos.)

$$G = 6.67\times 10^{-11} \dfrac{N·m^2}{kg^2}$$

📌 $M$ y $m$ son las masas de los cuepos que interaccionan.

📌 $r$ es la distancia que los separa.

La expresión de la ley de la gravitación universal, únicamente sirven para masas puntuales y cuerpos esféricos, ya que estos se comportan como si toda su masa se concentrara en su centro. Por tanto, la distancia se mide desde sus centros.

Consecuencias de la ley de gravitación universal

La atracción que ejercemos sobre la Tierra

Las fuerzas gravitacionales, como fuerzas que son, obedecen el principio de acción reacción o tercera ley de Newton, por lo tanto:

¿Entonces por qué la Tierra no nos persigue cuando nos alejamos del suelo? Nuestra masa es muy inferior a la de la Tierra, por lo que cuando la fuerza gravitacional actúa sobre la Tierra y sobre nosotros, ella se mueve extremadamente poco hacia nosotros (despreciable) y nosotros mucho hacia ella. No es lo mismo aplicar la misma fuerza a un carro vacio que un lleno y que posee más masa. Obviamente el vacío se moverá más rápido.

La gravedad no depende de la masa de los cuerpos

Si un cuerpo de masa m se encuentra a una altura h sobre la superficie de la Tierra, la fuerza gravitacional que actúa sobre él es:

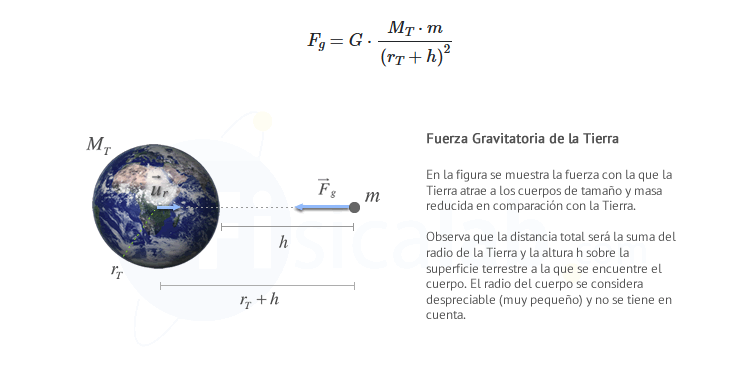
De acuerdo con la segunda ley de Newton, esta fuerza gravitatoria imprimirá una aceleración en el cuerpo, de tal forma que:

$$F_g = G \times\dfrac{M_T\cdot m}{{r_t}^2} = m \cdot a \Rightarrow a = G \times\dfrac{M_T}{{r_t}^2}$$

Esta aceleración ($a$) es lo que comúnmente llamamos gravedad y representamos con la letra $g$. ($g=9.8 \dfrac{m}{s^2}$).

Recuerda. Definición de Newton

Unidad de fuerza del Sistema Internacional, de símbolo N, que equivale a la fuerza que hay que aplicar a un cuerpo que tiene una masa de un kilogramo para comunicarle una aceleración de un metro por segundo cuadrado

El Newton es la la fuerza que se ejerce sobre un cuerpo de un $kgm$ (kilogramo masa) para adquirir una aceleración de:

$1\ \dfrac {m}{s^2}$ , o sea que $\quad 1\ N = 1\ kgm \cdot 1\ \dfrac {m}{s^2}$

en cambio el peso es una fuerza, y lo medimos en $kgf$, y equivale al peso de un $kgm$, para obtener el $kgf$, multiplicamos el $kgm$ por la aceleración de la gravedad, es decir:

$1\ kgf = 1\ kgm \cdot (9,81\ \dfrac {m}{s^2})$ por lo tanto,

$1\ kgf = 9,81\ kgm \cdot 1\ \dfrac {m}{s^2} = 9,81 \ kgm \cdot \dfrac {m}{s^2}= 9,81\ N$.

El kilogramo fuerza es $9,81$ veces mayor que el Newton.

🌍 ¿Cuál es la diferencia entre masa y peso?

🔹 Masa:

• Es la cantidad de materia que tiene un objeto.
• No cambia, sin importar dónde estés: en la Tierra, Marte o el espacio.
• Se mide en kilogramos ($kg$).
• Es una propiedad intrínseca del cuerpo, como su tamaño o volumen.

🔹 Peso:

• Es la fuerza con la que un planeta (como la Tierra o Marte) atrae un objeto debido a la gravedad.
• Cambia dependiendo de dónde estés. Si estás en Marte, pesas menos que en la Tierra.
• Se mide en newtons ($N$).
• Se calcula con la fórmula:
• 📐 $Peso = Masa × Gravedad$